在了解红黑树之前,我们必须先了解二叉搜索树(又称二叉排序树,我在上一篇文章中有介绍),因为红黑树是一种特殊的二叉排序树:在每个节点上增加一个存储位来表示节点的颜色,因此红黑树共有五个域:color,key,lchild,rchild,p。
红黑树的提出:一个高度为h的二叉排序树可以实现任何一种基本的动态集合操作:插入、删除、查找等操作,但是当树才高度比较高时,二叉树就会退化成链表。而红黑树能确保在最坏的情况下,基本的动态集合操作的时间为$O(logn)$.
红黑树的性质决定了红黑树的性能,红黑树共有五大性质:
1、 每个节点不是红的,就是黑的。
2、 根节点是黑的。
3、 每个叶节点都是黑的。
4、 若一个节点是红的,则他的子节点都是黑的。
5、 对于每个节点,从该节点出发到其子孙叶节点的所有路径上包含相同数目的黑节点。
图片的信息比笔述更加清新明了,下图1-3就是一棵红黑树的几种形式:
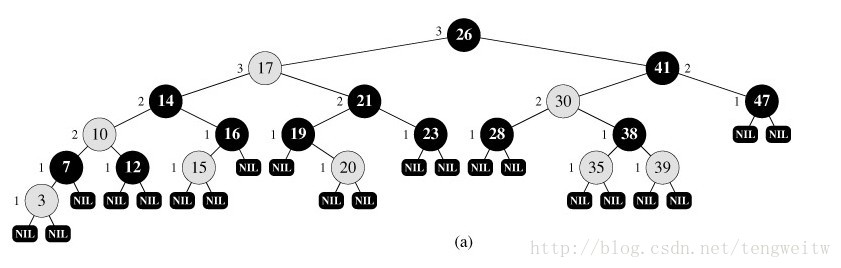
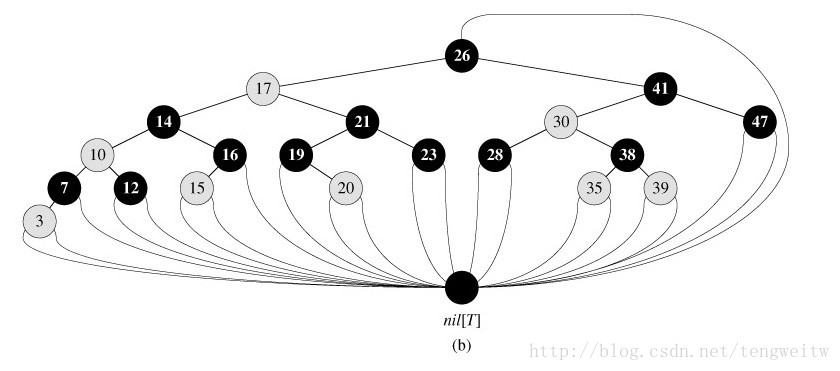
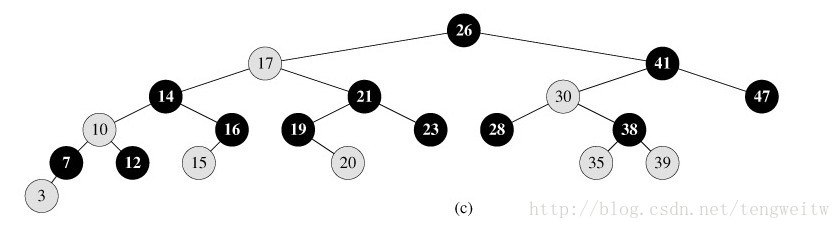
上图中,为了便于处理边界问题,我们采用一个哨兵来代表NIL。哨兵NIL是一个与普通节点有相同域的对象。它的color域为BLACK,其它域可随意设置。我在程序中将p、lchild、rchild设置为NULL,将key设置为-1.将所有指向NIL的指针都指向哨兵NIL。
下面先说明两个概念:内节点和外节点
内节点:把带关键字的节点称为内节点。
外节点:把没有子节点或父节点的节点称为外节点,我们把外节点都看成是哨兵NIL。
由于我们关注的是关键字key,因此我们主要关心内节点,所以在画红黑树的时候,常常忽略叶子,如上图3所示。
在介绍红黑树的插入和删除前,我们先必须介绍旋转这个概念。因为它在红黑树的插入、删除中,要用到很多。
旋转:分为左旋、右旋,它能够保持二叉排序树性质的局部操作。至于为什么能够保持性质,我也没有深入研究。前人不知道怎么发现这个操作。
我始终认为图像更能直观的表达更准确丰富的含义,我相信大家通过下图即可以明白左旋和右旋了。
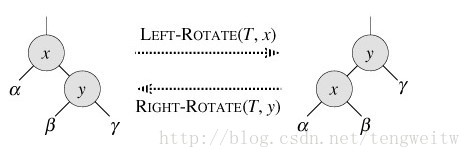
如果对上图4还是不太明了,也没关系,具体举例能使你有更深刻的认识,下图5是在x上左旋的过程:
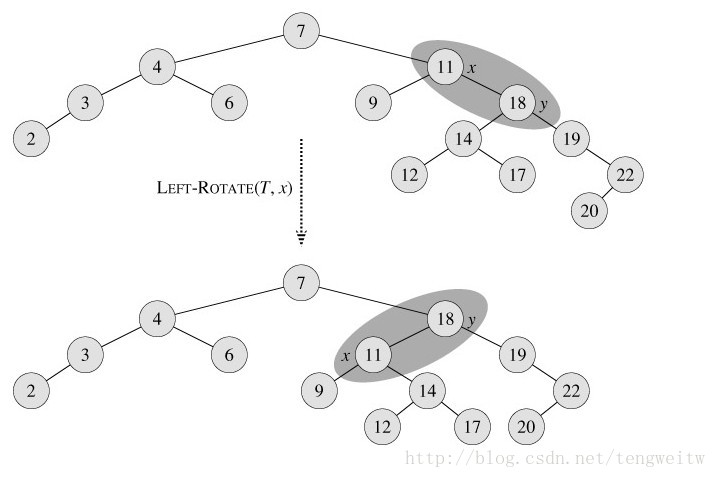
下面附上左旋和右旋的代码:
1 | /*************************************************\ |
插入操作:插入函数和插入修正函数
在前一篇文章中我已经介绍了二叉排序树,其中也有插入和删除操作。因为红黑树也是二叉排序树,因此其插入操作大同小异,不同之处在于,红黑树的性质会被插入和删除操作所破坏,因此就需要修正。修正包括两个操作:重新着色、旋转。
从上面的分析可知,红黑树的插入操作分为两步,首先像二叉排序树一样进行插入操作,然后调用修正函数来保持红黑树的性质。在插入操作中,我们都设置插入节点的color域为红而不是黑(如果是黑的话,性质4就不会破坏),为什么?请读者好好思考。下面为插入函数的实现:
1 | /*************************************************\ |
在Insert_FixUp插入修正函数中,循环截止条件为 z->p是黑色。如果z->p是红色,显然这就违返了红黑的树性质4。在循环中,我们要讨论6种情况,但是其中三种与另外三种是相互对称的,它可以由插入节点的父节点为祖父节点的左孩子还是右孩子来区分。下面我只讨论插入节点的父节点为祖父节点的左孩子的情况。在每一次迭代中,我们可能遇到以下三种情况。
情况一:叔叔是红色的
这时只要把插入节点z的父亲z->p和uncle都设成黑色,并把祖父z->p->p设成红色。这样仍然确保了每一条路径上的黑色节点数不变。然后把z指向z->p->p,并开始新一轮的迭代。如下图6: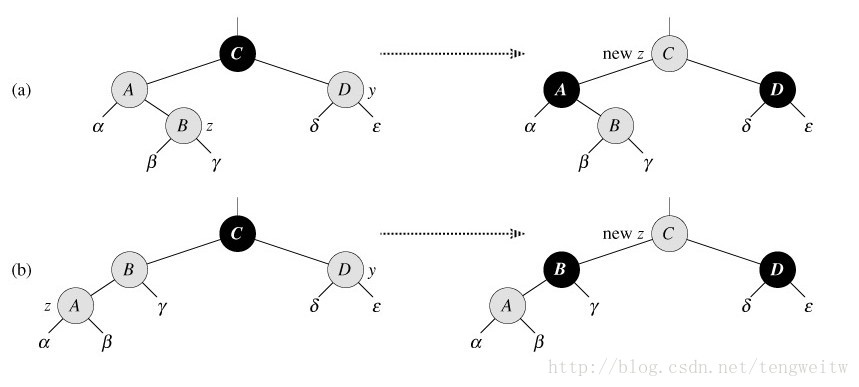
- 情况二:叔叔是黑色的情况下,插入节点为右孩子
这时我们只要把z指向z->p,然后做一次Left-Rotate(z)。就可以把情况转化成情况三。
- 情况三:叔叔是黑色的情况下,插入节点为左孩子
只要把z->p设成黑色,把z->p->p设成红色,然后就调用 Right_Rotate(z->p->p),整棵树就修正了。情况二和情况三如下图: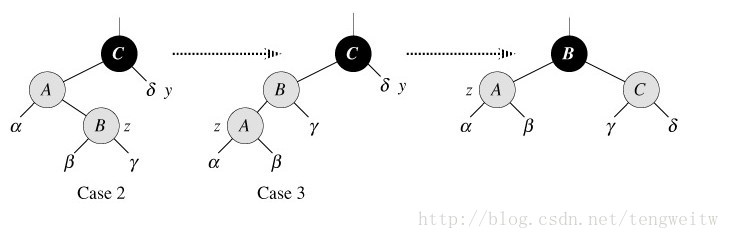
插入修正函数的具体实现如下:
1 | /*************************************************\ |
删除操作:删除函数和删除修正函数
删除操作和插入操作一样,都可以和二叉排序树一样进行对比。红黑树的删除操作分为两步,首先像二叉排序树一样进行删除操作,然后调用修正函数来保持红黑树的性质。前一篇二叉排序树的文章也讲过,删除操作要比插入操作复杂一些,红黑树也不例外。删除函数的具体实现如下:
1 | /*************************************************\ |
在Del_FixUp删除操作修正函数中,循环截止条件为z->color== RED。如果z->p是黑色,即删除的节点为黑色,显然这就违返了红黑的树性质5。在循环中,我们要讨论8种情况,但是其中4种与另外4种是相互对称的,它可以由删除的节点为父节点的左孩子还是右孩子来区分。下面我只讨论删除的节点为父节点的左孩子的情况:
在每一次迭代中,我们可能遇到以下4种情况:
情况一:兄弟为红色
这时我们根据红黑树的性质可以肯定删除的节点x->p是黑色、其兄弟节点w->lchild是黑色。我们把x->pt与brother的颜色互换,然后做一次Left-Rotate(x->p)。做完之后x的新的兄弟:原w->lchild,是黑色的。因此我们在不破坏红黑树性质的前提下,把情况一转换成了情况二、情况三、情况四中的一个,如下图8: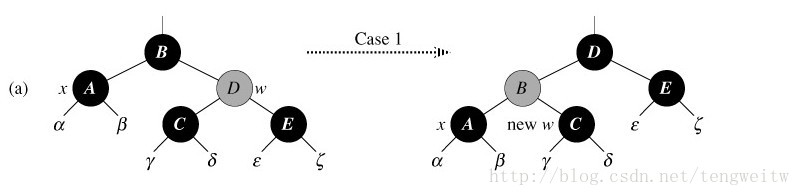
情况二:兄弟为黑色,其两个孩子为黑色
这时我们只要把w设成红色,然后把x移到x->p,这一次操作不会破坏红黑树的性质。如下图9(图中节点B不一定是红色,也可能是黑色):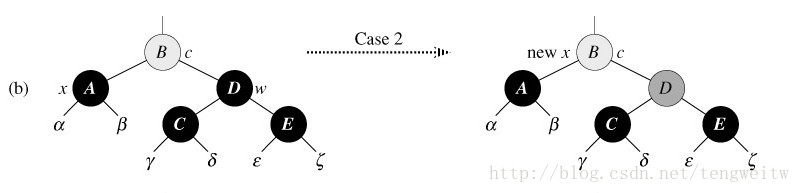
情况三:兄弟为黑色,且其左孩子为红色,右孩子为黑色
我们把w与w->lchild的颜色互换,然后做Right-Rotate(w)。这样做不会破坏红黑树的性质。这时x的新的兄弟就是原w->lchild。而情况3被转化成了情况4,如图10: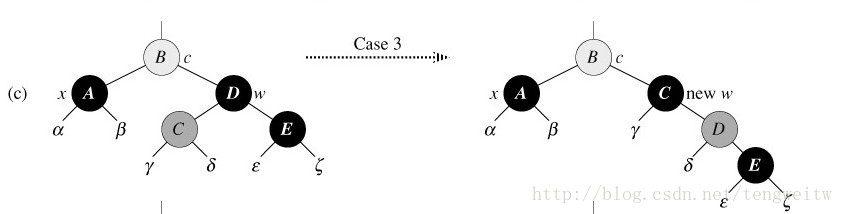
情况四:兄弟为黑色,且其右孩子为红色
先把w与x->parent的颜色互换,再做Left-Rotate(x->parent)。这时图中节点E(也就是原w->rchild)所在的路径就肯定少了一个黑色,而x所在的路径则多了一个黑色。那么我们就把使E也为黑色,这样就保持了红黑树的性质。如下图11:

具体的代码实现如下:
1 |
|
实验结果
最后给出运行结果的说明:在我电脑上的运行结果为:
(key为关键字,color=0表示为红色,color=1表示为黑色,key=-1代表空节点)
插入节点的关键值为11
插入修正前的广度遍历:
key=11 color=0
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为2
插入修正前的广度遍历:
key=11 color=1
key=2 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为14
插入修正前的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为1
插入修正前的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=0
key=1 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为7
插入修正前的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=7 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=7 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为15
插入修正前的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=7 color=0
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=7 color=0
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为5
插入修正前的广度遍历:
key=11 color=1
key=2 color=1
key=14 color=1
key=1 color=0
key=7 color=0
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=5 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=1
key=1 color=1
key=7 color=1
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=5 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为8
插入修正前的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=1
key=1 color=1
key=7 color=1
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=5 color=0
key=8 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入修正后的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=1
key=1 color=1
key=7 color=1
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=5 color=0
key=8 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
插入节点的关键值为4
插入修正前的广度遍历:
key=11 color=1
key=2 color=0
key=14 color=1
key=1 color=1
key=7 color=1
key=-1 color=1
key=15 color=0
key=-1 color=1
key=-1 color=1
key=5 color=0
key=8 color=0
key=-1 color=1
key=-1 color=1
key=4 color=0
插入修正后的广度遍历:
key=7 color=1
key=2 color=0
key=11 color=0
key=1 color=1
key=5 color=1
key=8 color=1
key=14 color=1
key=-1 color=1
key=-1 color=1
key=4 color=0
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=15 color=0
插入操作完成!!
形成的红黑树为:
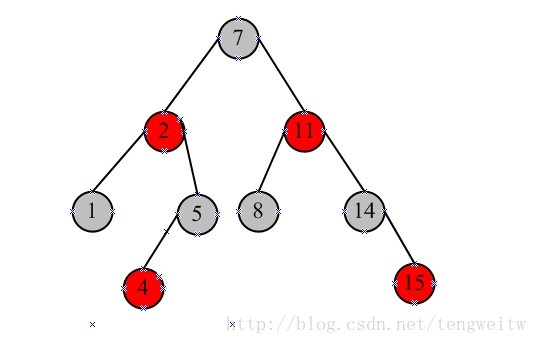
删除节点的关键值为5
删除顶节点后的广度遍历:
key=7 color=1
key=2 color=0
key=11 color=0
key=1 color=1
key=4 color=1
key=8 color=1
key=14 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=-1 color=1
key=15 color=0
请按任意键继续. . .
删除节点5后的红黑树为:
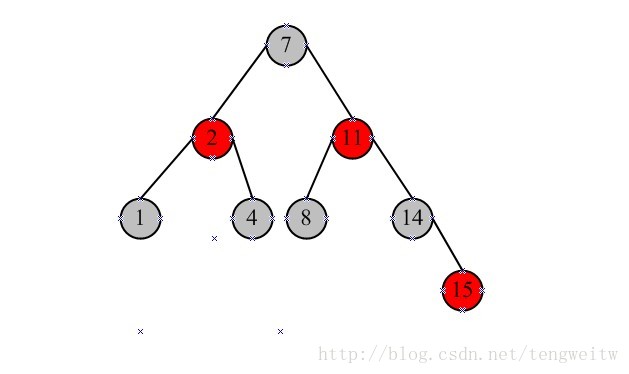
本文参考资料:《算法导论》

