本文讲解的不是离散分布的一些性质如:方差、期望和概率密度函数pdf(若为离散分布,则是概率质量函数pmf)等。本文要讲解的是如何通过均匀分布来产生其他各种分布的方法。尽管很多编程语言的函数库中包含了这些分布函数:
在matlab中,我们可以看到关于这些函数的详细文档及使用方法:
在linux C中,GNU有一个名字叫GUN Scientific Library的库,里面有各种分布函数,比如说,高斯分布:
http://www.gnu.org/software/gsl/manual/html_node/The-Gaussian-Distribution.html在标准C中,就只有仅仅的rand函数来产生均匀分布,那么这时候就需要使用均匀分布来产生其他分布了。
在下文中,我只是用比较通俗易懂的方式来说明用均匀分布来产生各种其他分布的过程,从而知道如何编程实现,具体原理的证明以及各种分布函数的性质就不具体展开。
离散分布
离散分布主要有以下几种:均匀分布、超几何分布、二项分布、泊松分布、负二项分布、几何分布
基本原理:
对于一个给定的离散分布,我们假设其分布如下:有$n$个离散的取值分别为${x1},{x_2},\cdots ,{x_n}$,他们的概率分别为${P}, {P}, \cdots, {P}$,并且有${P} + {P}+ \cdots + {P_} = 1$,设该离散分布的分布函数为$F(x)$,那么,我们可以通过如下步骤来产生该离散分布:
- 产生区间在$[0, 1]$的均匀分布${U}$
- 当$F(xi)<U\le F(x{i + 1})$时,令$X$=$x_{i+1}$,这时$X$的取值就服从上述给定的离散分布。
上述理论很简单,不过为了更简单明了的说明上述原理步骤,下面通过举例来具体描述:
假设离散分布如下:$x$的可能取值分别为$1,2,3$,对应的概率分别为$\frac{1}{4}$,$\frac{1}{4}$,$\frac{1}{2}$。那么其分布函数$F\left( \right)$可以表示如下:
那么通过均匀分布产生上述离散分布的方法由步骤2可知如下式:
其中,由分布函数$F(x)$的表达式可知,$F\left( \right) = \frac{1}{4},F\left( \right) = \frac{1}{2},F\left( \right) = 1$,带入到上式中可知,$x$取值分别为$1,2,3$时,对应的概率分别为$\frac{1}{4}$,$\frac{1}{4}$,$\frac{1}{2}$,即服从上面指定的离散分布。
从上面的方法可以看出,只要知道了离散随机变量在各个点的概率就可以使用该方法,通过均匀分布得到指定的分布了。而各个点的概率可以通过概率质量函数(pmf)得到。关于各种离散分布的pmf,我们可以在维基百科上得到。下面通过上面提到的方法,分别以二项分布、泊松分布为例进行Matlab编程实现:
二项分布
1 | clear all |
运行结果如下: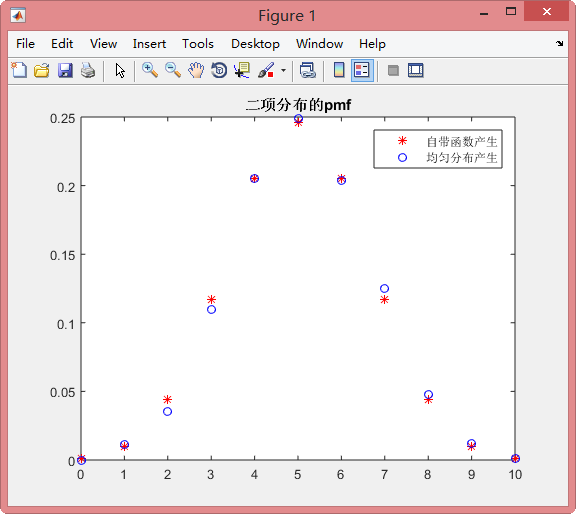
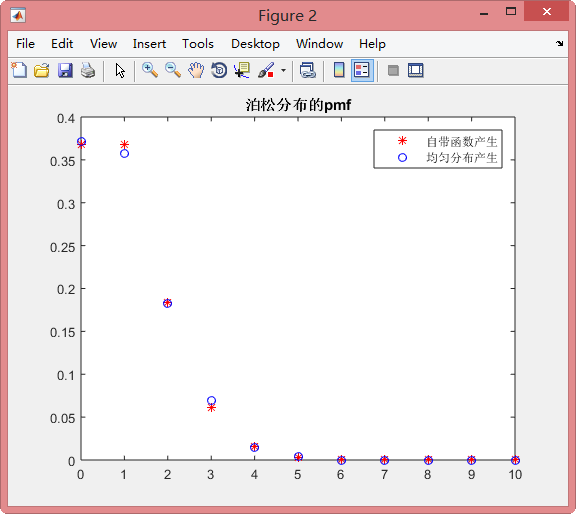
泊松分布
每个分布的实现大致相同,只需要更改计算pmf的公式即可!由于泊松分布在实际问题中非常常见,因此在此赘述。
1 | %泊松分布 |
显示结果如下:(到达率$\lambda=1$时)