支持向量机(Support Vector Machine, SVM),是一种常见的有监督的学习模型,通常用来进行模式识别、分类以及回归分析。本文主要介绍SVM在二分类问题的应用。
线性可分支持向量机
我们还是以【图解例说机器学习】感知机的二分类例子 (Toy Example) 说起。如图1,假设有一个线性可分的训练集,其中有三个样例 ($\mathrm x_1,\mathrm x_2, \mathrm x_3$),分别标记为正例(红色方块),反例(蓝色圆圈)。这里的 $x^{(1)},x^{(2)}$为训练样例的$2$个特征。
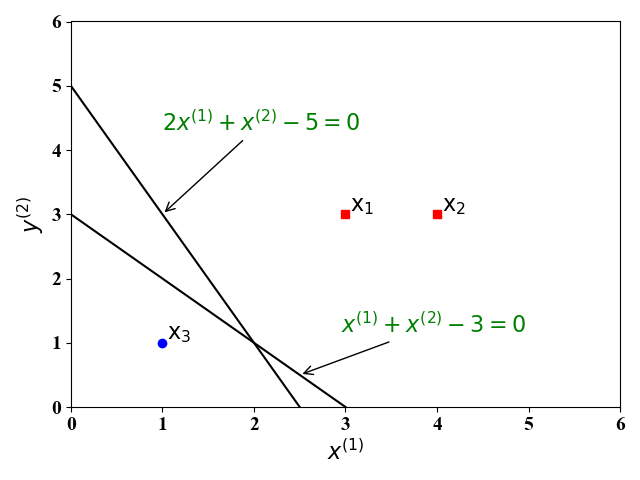 |
感知机的目的就是找到一个超平面 (在二维空间为一条直线) 能够将这三个样例分开。显然,这样的直线有无数条,比如图中的直线 $f(\mathrm x)=x^{(1)}+x^{(2)}-4=0, f(\mathrm x)=2x^{(1)}+x^{(2)}-5=0$ 就是可能得到其中的两条。
感知机的结果,即分类超平面,与参数的初始值有关,也和在每次迭代时选取的误分类样例有关。在上面例子中,得到的两个分类超平面中,直觉上,直线$x^{(1)}+x^{(2)}-4=0$的分类效果要好于$2x^{(1)}+x^{(2)}-5=0$的分类效果好。这是因为,直线$x^{(1)}+x^{(2)}-4=0$位于正负样例的中间位置,其对训练样例的扰动具有较好的鲁棒性。由于训练集的局限性或者噪声,训练集外的样例可能比较接近分类超平面,此时直线$2x^{(1)}+x^{(2)}-5=0$就会使得这些样例错误分类,即泛化能力较差。
为了克服感知机的上述问题,SVM的目的就是找到最佳的分类超平面,而不是仅仅对训练集的样例正确分类,也考虑如何对未见样例具备较强的泛化能力。
SVM 分类模型
间隔
在中学时,我们学过一个点$x$到一条直线$ax+by+c=0$的距离可以为$\lvert ax+by+c\rvert/\sqrt{a^2+b^2}$。类似地,空间中一点$\mathrm x$ 到一个超平面$\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$的距离为:
关于公式(1)的直观表示如下图2所示:
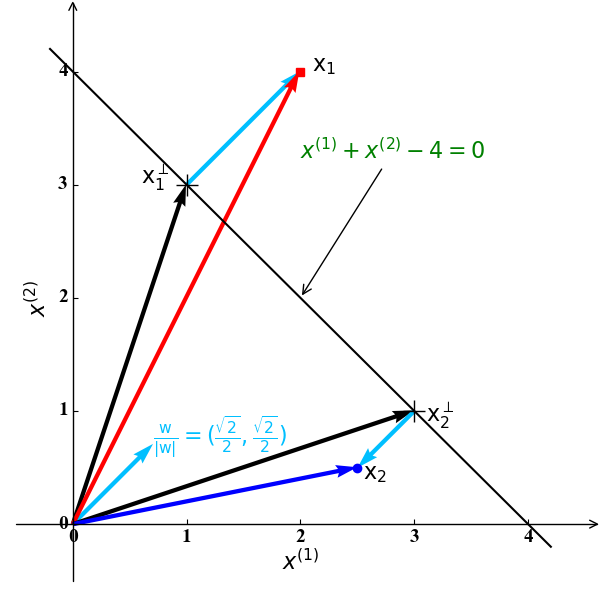 |
在图2中,$\frac{\mathrm w}{\lvert\mathrm w\rvert}$ 是直线$x^{(1)}+x^{(2)}-3=0$的单位法向量,$\mathrm x_1^\perp, \mathrm x_2^\perp$ 分别为$\mathrm x_1, \mathrm x_2$ 在该直线的投影。此时空间中的任意一点$\mathrm x$可以由其到该直线的投影$\mathrm x^\perp$ 和单位法向量表示:
对于公式(2),我们将其乘以$\mathrm w$ 加上$\omega_0$ 后有:
由于$\mathrm x^{\mathrm T}$ 是直线$\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$ 上的点,由公式(3)可得:
结合图2和公式(2)和(3),我们可以表示$\mathrm x_1,\mathrm x_2$如下:
公式(5)和(6)表明:当$\mathrm x$为正例 (例如 $\mathrm x_1$) 时,$d$为正数;当$\mathrm x$为反例 (例如 $\mathrm x_2$) 时,$d$为负数。也就是说,公式(4)中的距离$d$是有方向的。具体来说,对于例子中的样例$\mathrm x_1$,是正例,即$y=+1$ ,其到直线 $\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$ 的距离为$d=\frac{\mathrm w^{\mathrm T}\mathrm x_1+\omega_0}{\lvert\mathrm w\rvert}>0$; 对于例子中的样例$\mathrm x_2$,是反例,即$y=-1$ ,其到直线$\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$的距离为$d=\frac{\mathrm w^{\mathrm T}\mathrm x_2+\omega_0}{\lvert\mathrm w\rvert}<0$.为此,对于任意样例$\mathrm x$ (无论正例还是反例),其距离分类超平面的无方向距离(始终大于0)为:
注意:公式(7)是公式(6)在考虑样例分类情况下,将有方向的距离$d$化为无方向距离$\lvert d\rvert$的具体表达式。
优化问题
SVM的中心思想就是找出离分类超平面最近的点(又称支持向量),然后最大化这些点与分类超平面的距离。对于一个$M$维特征空间,超平面的表达式为:
为此,我们可以得到如下的优化问题:
直接求解问题(9)比较复杂。这里我们发现,对于一个分类超平面 (例如,上面例子中的直线$\hat y=\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$ ),同时对$\omega_0,\mathrm w$进行缩放并不改变该分类超平面,也就不改变任意点到该分类超平面的距离。为此我们可以将$\omega_0,\mathrm w$进行缩放,使得离分类超平面最近的点 (支持向量)满足$(\omega_0+\mathrm w^{\mathrm T}\mathrm x)y=1$。那么此时,训练集中所有其他样例点肯定满足$(\omega_0+\mathrm w^{\mathrm T}\mathrm x)y>1$。这时,优化问题(9)可以转化为SVM优化问题的标准形式:
注意:问题(9)转为标准形式(10)的主要步骤:1)令支持向量对应的$(\omega_0+\mathrm w^{\mathrm T}\mathrm x)y=1$,从而去掉最小化,并将问题(9)中的分子加入到约束中;2)最小化$\frac{1}{\lvert\mathrm w\rvert}$等效于最大化$\frac{1}{2}{\lvert\mathrm w\rvert^2}$。
从标准化的优化问题可以看出,该问题是凸二次优化问题,可以使用一些已有的工具箱求解,如CVX, Gurobi, CPLEX等。
基于CVX的问题求解
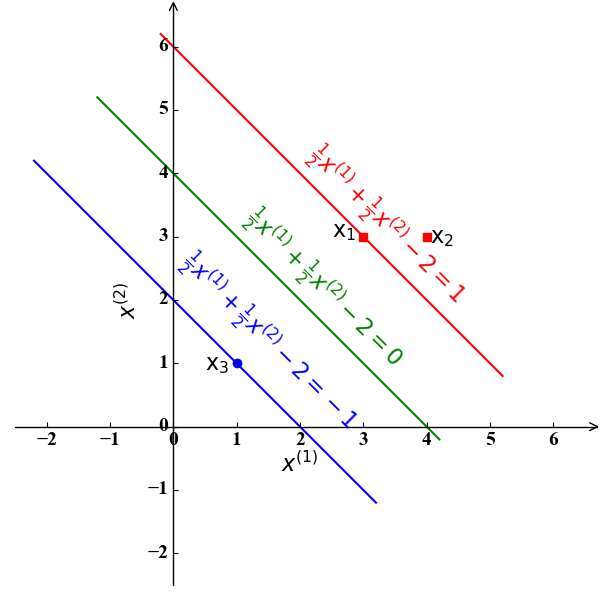
我们还是以本文开始的小例子 (Toy Example) 为例。此时,我们得到的分类超平面应该是一条直线,形式为$\omega_0+\omega_1x^{(1)}+\omega_2x^{(2)}=0$。根据SVM的标准凸优化形式(10),我们有
求解该问题,我们可以得到其最优解为$\omega_0=2,\omega_1=\omega_2=\frac{1}{2}$。此时的分离超平面为直线$\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=0$。此时的决定该直线的支持向量为使得$\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=1,-1$的样例点$\mathrm x_1(3,3)$和$\mathrm x_3(1,1)$。下图3具象地表达了这一结果:
 |
关于CVX算法实现部分,由于这台电脑没有装MATLAB,此部分回学校后再写
至此,最基本的SVM算法已经讲完了。由于上述SVM存在一些难点,下面我们对其进行扩展:
- SVM标准形式的凸优化问题不易求解,往往我们可以通过其对偶问题求解
- 当训练集的样例线性不可分,而通过投影到高维空间后线性可分时,我们可以在对偶问题中使用核函数
- 当训练集及其高维映射都不可分时,我们可以考虑容许部分样例分类错误
对偶问题
为例求解上述标准形式的凸二次优化问题(10),我们除了使用工具箱直接求解外,还可以通过其对偶问题求解。一般来说,相对于求解原始问题,求解其对偶问题一般有以下好处:1)即使原始问题不是凸的,对偶函数仍是关于对偶变量的凸函数;2)具有更好的解释性,适用于分布式算法。对于SVM问题,我们发现求解其对偶问题的过程中可以使用核函数 (下一节提及),可以使用一些启发式算法 (后文提及的SMO) 来加速算法。
对约束引入拉格朗日乘子$\lambda={\lambda_i\ge 0\mid i=1,2,\cdots,N}$,我们得到如下的拉格朗日函数:
此时对应的对偶问题为:
由于原始问题(10)为凸问题,那么对偶问题与原始问题的解的gap为0. 通过求解对偶问题,我们就能得到原始问题的最优解。
求解上述对偶问题 (极大极小问题) 的一般思路为,先固定$\lambda$ ,求解 $\min\nolimits{\omega_0,\mathrm w}\quad L(\omega_0,\mathrm w\mid \lambda)$得到$\omega_0,\mathrm w$,然后一般通过梯度(或次梯度)更新$\lambda$。幸运地是,在求解 $\min\nolimits{\omega0,\mathrm w}\quad L(\omega_0,\mathrm w\mid \lambda)$ 时,我们可以得到其解析解 $\omega_0^\star,\mathrm w^\star$,所以我们不需要迭代,只需要直接求解$\max\nolimits{\lambda}\quad L(\lambda\mid \omega_0^\star,\mathrm w^\star)$。具体步骤如下:
求解$\min\nolimits_{\omega_0,\mathrm w}\quad L(\omega_0,\mathrm w\mid \lambda)$
由于该问题为凸二次规划问题,其最优解为一阶微分为0的点,即:将公式(14)和(15)带入公式(10),我们有:
求解$\max\nolimits_{\lambda}\quad L(\lambda\mid \omega_0^\star,\mathrm w^\star)$
在求得参数$\mathrm w^\star$后,我们需要求解如下问题:由公式(14)和(16)可以等效成如下问题:
将问题(18)向量化可得:
最终,我们需要求解问题(19),当然由于问题(19)也是一个凸二次函数,我们同样可以利用工具箱求解,在此省略。求解问题(19)得到最优的$\lambda$后,我们将(14)带入超平面的表达式(8)中得到:
当对一个新的测试样例$\mathrm x$ 进行分类时,可以由上式可以判断:当$\hat y\ge1$ 时,判断为正例;当 $\hat y\le -1$ 时, 判断为反例。当然,上述问题在于$\omega_0$ 的值还无法得知。为此,我们可利用KKT条件(这里不具体描述,有需要会后续单独介绍)可得:
由互补松弛条件(23)可知,要么$\lambda_i=0$,要么 $y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1$。从分类超平面的表达式(20)可知,只有当$\lambda_i>0$时,才对分类结果$\hat y$ 有影响,此时的样例点$\mathrm x_i$ 才对决定了分类超平面的表达式,这样的样例点就是我们所说的支持向量。当$\lambda_i>0$时, 由(23)知$y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1=0$,也就是对应了图3所示的支持向量所在的超平面。那么这时,由$y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1=0$ 我们就有
下面我们同样通过上述的小例子来验证对偶算法的可行性:
根据对偶问题的形式(18)或(19),小例子对应的对偶问题可以写成:
为了求解问题(25),我们替换变量$\lambda_3=\lambda_1+\lambda_2$可得
令$L(\lambda_1,\lambda_2)$ 对于$\lambda_1,\lambda_2$ 的偏导为0,可知最优的解为$\lambda_1^\star=\frac{3}{2},\lambda_2^\star=-1$,不满足$\lambda_2\ge 0$。为此,最优解在边界处取得。若$\lambda_1^\star=0$,此时$\lambda_2^\star=\frac{2}{13}$,最优值为$L(\lambda_1^\star,\lambda_2^\star)=-\frac{2}{13}$。若$\lambda_2^\star=0$,此时$\lambda_1^\star=\frac{1}{4}$,最优值为$L(\lambda_1^\star,\lambda_2^\star)=-\frac{1}{4}$。所以,最终得到的最优解为$\lambda_1^\star=\frac{1}{4},\lambda_2^\star=0,\lambda_3^\star=\frac{1}{4}$。
在得到最优解$\lambda^\star={\lambda_1^\star,\lambda_2^\star,\lambda_3^\star}$后,我们可以根据等式(14)求得$\omega_1=\omega_2=\frac{1}{2}$。又由于$\mathrm x_1,\mathrm x_3$为支持向量,由公式(25)我们有:
由(27)或者(28)我们可以得到$\omega_0^\star=-2$。那么我们求得的最优分类超平面为直线$\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=1$。
我们发现,最后需要求解的对偶问题为(19),也是一个凸二次优化问题。一般来说,二次优化问题的算法复杂度为$\mathcal O(K)$,其中$K$为变量的个数。在原始问题(10)中,变量为$\omega_0,\mathrm w$,个数为$M+1$;在对偶问题(19)中,变量为$\lambda$,个数为$N$。注意:这里的$M,N$分别为特征维数和样例个数。一般情况下,样例数大于特征维数,即($N>M$),此时好像更应该直接求解原始问题来降低复杂度。但是由于对偶问题的特性比较适合核函数的使用,我们更倾向于求解对偶问题。
核函数
在上述模型中,我们假设训练集是线性可分的。但一般情况下,原始的特征空间是线性不可分的,如下面的两个例子:
异或问题:假设我们考虑2个特征$x^{(1)},x^{(2)}$,训练集中有两个正例 $\mathrm x_1 (0,1), \mathrm x_2 (1,0)$ 和两个反例 $\mathrm x_3 (0,0), \mathrm x_4 (1,1)$,如图4所示。显然,我们无法在该二维空间中找到一条直线将训练集正确分类。如果我们将这两个特征$x^{(1)},x^{(2)}$映射到三维空间的三个特征$z^{(1)},z^{(2)},z^{(3)}$, 且映射关系为: $z^{(1)}=x^{(1)}x^{(2)}, z^{(2)}=x^{(1)}, z^{(3)}=x^{(2)}$。那么此时训练样例坐标为:$\mathrm x_1 (0,0,1), \mathrm x_2 (0,1,0), \mathrm x_3 (0,0,0), \mathrm x_4 (1,1,1)$,如图5所示。显然,我们可以找到一个分类超平面将该训练集正确分类。
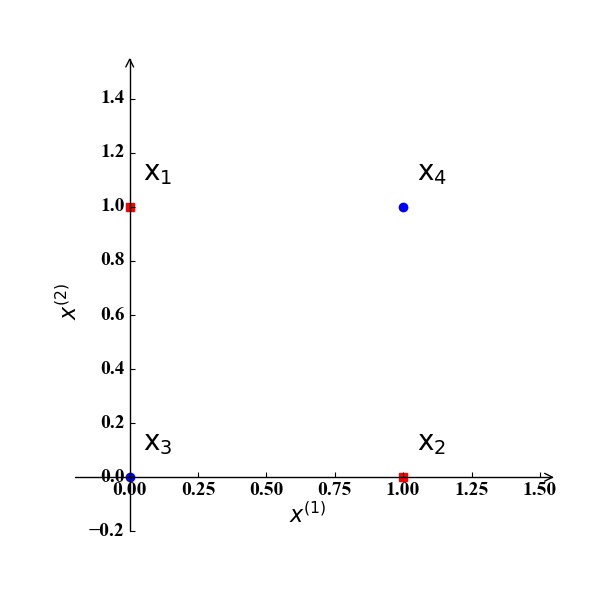 图4
图4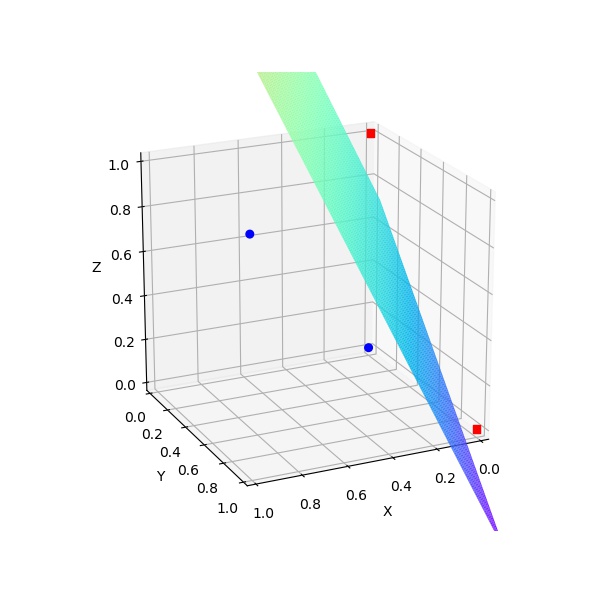 图5
图5
圆环问题:假设我们考虑2个特征 $\mathrm x={x^{(1)}, x^{(2)}}$,训练集由两个通过原点的同心圆 $\lvert \mathrm x\rvert^2=C$ 产生正例 ($C=3$) 和反例 ($C=1$),如图6所示。显然,我们无法在该二维空间中找到一条直线将训练集正确分类,此时的最佳分类超平面应该是一个圆环 $\lvert \mathrm x\rvert^2=2$ 。此时,若我们将这两个特征映射成两个新的特征 $z^{(1)},z^{(2)}$,且映射关系为 $z^{(1)}=[x^{(1)}]^2,z^{(2)}=[x^{(2)}]^2$,那么此时对应的最优分类超平面为直线$z^{(1)}+z^{(2)}=2$,如图7所示。
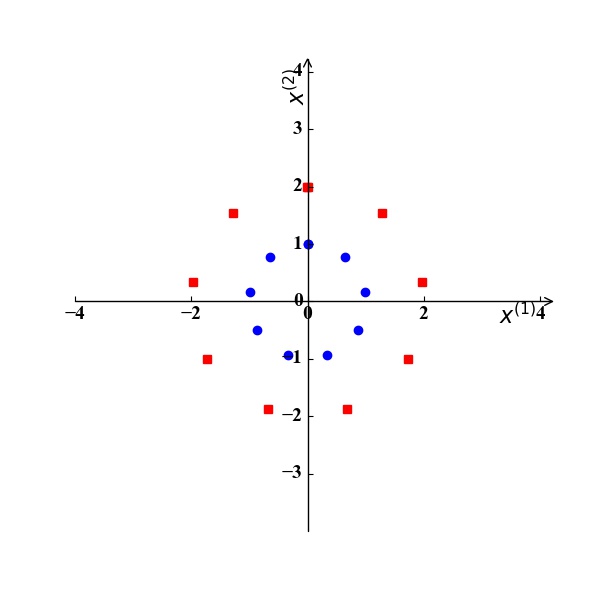 图6
图6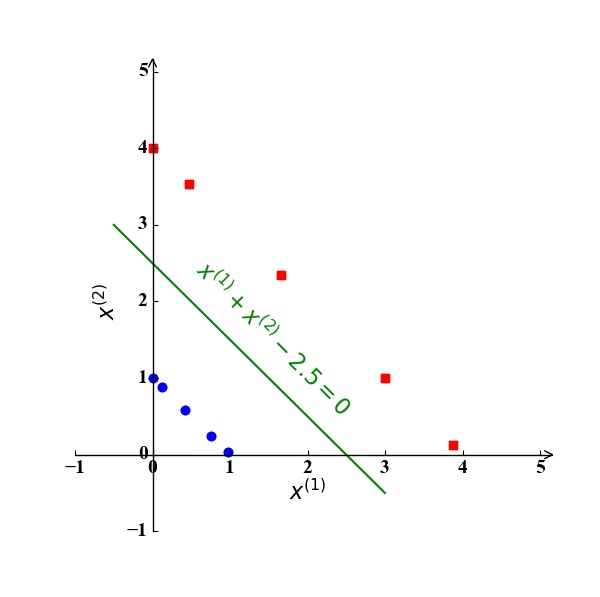 图7
图7
上面的两个例子说明,当原始的特征空间线性不可分时,我们可以将原始特征空间映射为新的特征空间,使其线性可分。这里,我们将上述的映射关系用数学表达式定义为
那么此时,经过特征映射后,优化问题(19)转化为:
为简便起见,我们定义
公式(31)就是我们提到的核函数。
那么这里难点在于如何找到好的映射函数和核函数,也就是公式(31)的表达式?对于上面的例子,由于十分简单,我们可以很容易的定义映射函数。然而,对于实际中比较复杂的训练集,我们一般采用下面几种比较常见的核函数:
| 名称 | 表达式 | 名称 | 表达式 |
|---|---|---|---|
| 线性核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=\mathrm xi^{\mathrm T}\mathrm x{i^\prime}$ | 高斯核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=\exp(-\frac{\lvert\mathrm xi-\mathrm x{i^\prime}\rvert^2}{2\sigma^2})$ |
| 多项式核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=(a\mathrm xi^{\mathrm T}\mathrm x{i^\prime}+b)^c$ | 指数核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=\exp(-\frac{\lvert\mathrm xi-\mathrm x{i^\prime}\rvert}{2\sigma^2})$ |
| Sigmoid核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=\tanh(a\mathrm xi^{\mathrm T}\mathrm x{i^\prime}+b)$ | 拉普拉斯核 | $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=\exp(-\frac{\lvert\mathrm xi-\mathrm x{i^\prime}\rvert}{\sigma})$ |
下面我们以一个具体的多项式核 $\mathcal k(\mathrm xi,\mathrm x{i^\prime})=(\mathrm xi^{\mathrm T}\mathrm x{i^\prime}+1)^2$ 来说明核函数的好处。这里我们考虑原始特征空间为二维,即$\mathrm x={x^{(1)},x^{(2)}}$。那么此时核函数可以表示为:
从公式(31)可以看出我们把原始二维特征空间映射到了六维特征空间。最终计算$\phi(\mathrm xi)^{\mathrm T}\phi(\mathrm x{i^\prime})$是两个六维空间向量的内积,需要6次加法和6次乘法。然而,我们可以直接通过核函数$\mathcal k(\mathrm xi,\mathrm x{i^\prime})=(\mathrm xi^{\mathrm T}\mathrm x{i^\prime}+1)^2$ 计算$\phi(\mathrm xi)^{\mathrm T}\phi(\mathrm x{i^\prime})$,此时只需要进行二维空间的内积,总共需要3次加法和3次乘法。也就是说,通过核函数,我们可以直接在原始特征空间计算结果,从而避免在映射后的高维特征空间中计算内积。
线性不可分SVM
最基本的SVM模型可以对原始特征空间线性可分的训练集进行正确分类,如我们开头提到的小例子。利用核函数,我们可以对于原始特征空间,线性不可分,而在映射的特征空间线性可分的训练集进行正确分类,如图4-7提到的例子。然而我们还会遇到原始特征空间线性不可分,映射后的特征空间也线性不可分,或者说我们找不到一个好的核函数使新的特征空间线性可分的情况。下面这部分内容就是考虑线性不可分的情况。
对于线性不可分的情况,一个比较基本的方式,就是不一定需要所有的训练样例都正确分类,我们可以容忍部分样例被错误分类。如图8所示:
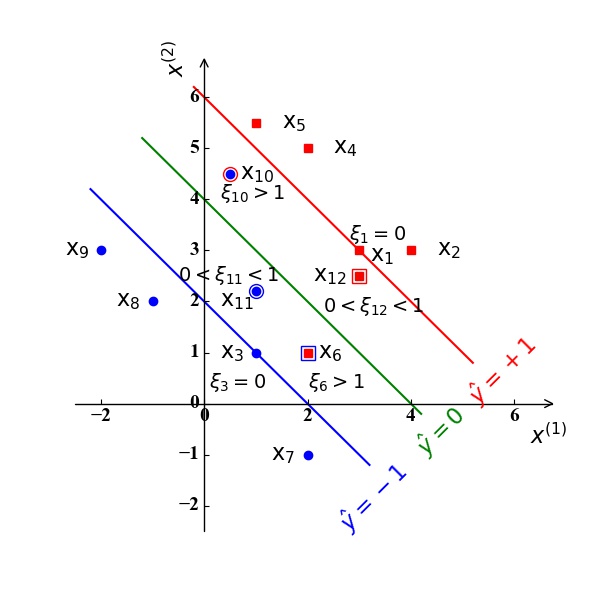 |
在图8中,我们假定分类超平面和支持向量和图3一样,即分类超平面为绿色直线$\hat y=\omega0+\mathrm w^{\mathrm T}\mathrm x=\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=0$ ,支持向量为$\mathrm x_1, \mathrm x_3$ 。样例点 $\mathrm x_6,\mathrm x{10},\mathrm x{11},\mathrm x{12}$ 位于直线 $\hat y=+1,-1$ 之间,即不满足我们前面提到的正确分类需要满足(10)中的约束, 其中,样例点 $\mathrm x6,\mathrm x{12}$ 被错误分类。
为了解决这一问题,我们可以为每一个样例点 $\mathrm x_i$ 引入一个松弛变量 $\xi_i\ge 0$ :
根据公式(33)我们可知:
- 位于 $\hat y=+1,-1$ 之外的样例点$\mathrm x_i,i=2,4,5,7,8,9$ 对应的松弛变量 $\xi_i=0,i=2,4,5,7,8,9$ 。
- 位于$\hat y=+1,-1$ 之上的样例点 (支持向量) $\mathrm x_i,i=1,3$ 对应的松弛变量 $\xi_i=0,i=1,3$ 。
- 位于$\hat y=+1,-1$ 之内的样例点$\mathrm x_i,i=6,10,11,12$ :
- 若其能正确分类,其对应的松弛变量 $0<\xi_i<1,i=11,12$ ;
- 若其被错误分类,其对应的松弛变量$\xi_i>1,i=6,10$ 。
此时问题(10)中的约束可变为:
由公式(34)可以看出,当样例$\mathrm x_i$ 被错误分类时,即 $(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)y_i\le 0$ ,此时对应的松弛变量为$\xi_i>1$ 。所以,松弛变量 $\xi_i$的引入是为了让所有的样例点都满足约束,使得带松弛的优化问题有解。但是,引入松弛变量容许样例点被错误分类,这并不是我们想要的结果。为此,我们需要在原问题(10)的目标(最大化间隔)基础上,考虑最小化错误分类带来的影响。这里我们一般最直观地,直接地使用 $\xi_i$作为引入松弛变量$\xi_i$ 带来的误差。因此,在原问题(10)的基础上我们有:
在优化问题(35)中,$C>0$ 是一个权重因子,用于平衡最大化间隔和最小化训练误差(即样例点被错误分类)。当 $ C \to \infty $ 时,相当于我们十分在乎训练误差,不容许训练样例被错误分类,此时所有的$\xi_i=0$。此时,问题(35)退化为问题(10)。
求解带松弛变量的优化问题
问题(35)也是一个凸二次优化问题,所以可以完全按照前面求解问题(10)的方式求解,在此我们只给出解析表达式。同样利用拉格朗日乘子法得到拉格朗日函数并对变量求偏导,令偏导为0,我们有:
在公式(38)中,$\lambda_i,\mu_i$ 分别为(35)中约束对应的拉格朗日乘子。将公式(36), (37)和 (38)带入问题 (35),我们有如下的对偶问题:
对比线性可分原问题(10)的对偶问题(19),这里的对偶问题(39)唯一的差别就是添加了约束 $\lambda_i\le C$。因此,问题(19)的解法与问题(39)的解法基本一致,并且前面所讲的核函数方法也同样适用。
求解问题(39)得到最优的$\lambda$后,我们将(36)带入超平面的表达式(8)中得到:
当对一个新的测试样例$\mathrm x$ 进行分类时,可以由上式可以判断:当$\hat y\ge0$ 时,判断为正例;当 $\hat y\le 0$ 时, 判断为反例。当然,上述问题在于$\omega_0$ 的值还无法得知。为此,我们可利用KKT条件可得:
由互补松弛条件(43)可知,要么$\lambda_i=0$,要么 $y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1+\xi_i=0$ 。从分类超平面的表达式(40)可知,只有当$\lambda_i>0$时,即$y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1+\xi_i=0$,才对分类结果$\hat y$ 有影响,此时的样例点$\mathrm x_i $ 才对决定了分类超平面的表达式,这样的样例点就是我们所说的支持向量,在图8中对应的支持向量为 $\mathrm x_i,i=1,3,6,10,11,12$ 。
当 $0< \lambda_i < C $ 时,由公式(38)知 $ \mu_i > 0 $,又由公式(44)可知,此时$\xi_i=0$,即该样例是位于 $\hat y=+1,-1$ 之上或之外的样例点。当$\lambda_i=C$ 时,有$\mu_i=0$: 此时若$\xi_i>1 $ ,该样例被错误分类,若$\xi_i\le1$,此时样例位于 $\hat y=+1,-1$ 之间,但是被正确分类的样例点. 这里的分析与我们前面对图8的解释一致。当$0<\lambda_i<C$时, 由(43)知 $y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1+\xi_i=0$ ,且$\xi_i=0$。那么这时有 $y_i(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1=0$ 我们就有
SMO算法
虽然对偶问题(19)和(39)都是凸二次函数,我们可以利用工具箱求解,在此省略。但是复杂度与样例成正比。当样例较多时,复杂度很高。为此我们介绍如何利用问题(39)的性质,使用SMO算法进行求解。SMO算法的主要思想本质上与坐标轮询法类似,即以一个变量$\lambda_i$ 为变量,其他$\lambda$ 固定来简化优化问题。也就是说,在参数$\lambda$ 初始化后,不断执行下列步骤直到收敛:
- 按照一定规则选取需要更新的 $\lambdai$ 和 $\lambda{i^\prime}$
- 固定除$\lambdai,\lambda{i^\prime}$的所有其他参数,求解简化后的问题(39)
从上述步骤可以看出,我们的重点在如何选择$\lambdai,\lambda{i^\prime}$以及如何求解问题(39)。
参数$\lambdai,\lambda{i^\prime}$ 的选择
对于一个凸二次优化问题,满足KKT条件是最优解的充要条件。为此,我们可以找一个违背该KKT条件的样例点对应的$\lambdai$作为需要更新的参数。对于另一个参数$\lambda{i^\prime}$ ,我们需要选择一个离$\lambdai$对应样例点较远的样例点,这样$\lambda_i$与$\lambda{i^\prime}$ 之间差别较大。这时,算法每次迭代都能有效地减少目标函数值。
解析解
当选择$\lambdai,\lambda{i^\prime}$作为我们的优化变量,问题(39)可以简化为(为表述简单,我们假定选择的变量为$\lambda_1,\lambda_2$ ) :
对于优化问题(46),我们首先分析其约束条件。由于只有两个变量,我们可以通过图像形象地表示如下:
图9和图10分别表示当$y_1\neq y_2$ 和 $y_1=y_2$时,变量$\lambda_1,\lambda_2$的取值范围和关系。
- 在图9中,即$y_1\neq y_2$,由问题(46)的约束我们有 $\lambda_1-\lambda_2=\eta$ 或 $-\lambda_1+\lambda_2=\eta$ ,此时$\lambda_2$的最小值$L=\max{0,-\eta}$,最大值为$H=\min{C,C-\eta}$ 。
- 在图10中,即$y_1= y_2$,由问题(46)的约束我们有 $\lambda_1+\lambda_2=\eta$ 或 $-\lambda_1-\lambda_2=\eta$ ,此时$\lambda_2$的最小值$L=\max{0,\eta-C}$,最大值为$H=\min{C,\eta}$ 。
综合起来也就是:
将问题(46)中的约束$\lambda_1y_1+\lambda_2y_2=\eta$ 同时乘以 $y_1$,我们有
当我们不考虑问题(46)中的约束 $0\le\lambda_i\le C$,且将变量$\lambda_1$由自变量$\lambda_2$ 表示后,问题(46)可以表示为:
将问题(49)中的常数项(不含变量$\lambda_2$ 的项 ) 删除不会影响最优解,且$y_1y_1=1$,于是我们有:
问题(50)是一个无约束的凸优化问题,为此,其最优解$\lambda_2^\star$满足: 目标函数关于$\lambda_2$ 导数为0,在此省略求导过程,直接给出最优解的解析表达式:
其中,训练样例误差$E1=\omega_0+\sum\limits{i=1}^{N}\lambdaiy_i\sum\limits{j=1}^{M}xi^{(j)}x_1^{(j)}-y_1, E_2=\omega_0+\sum\limits{i=1}^{N}\lambdaiy_i\sum\limits{j=1}^{M}x_i^{(j)}x_2^{(j)}-y_2$ 。
注意:公式(51)表明当最优的$\lambda_2^\star $ 与当前参数$\lambda_2$ 有关。换句话说,当$\lambda_2$ 不同时,得到的最优解$\lambda_2^\star $ 。这样我们可以通过不断迭代(51)可以最终使得$\lambda_2^\star $不变,即收敛。即,在第$t$ 次迭代初,我们知道所有的参数值$\lambda$ ,然后根据(51)更新$\lambda_2$,重复该迭代过程,直至收敛。另一方面,当我们考虑(47)中$\lambda_2$ 的取值范围,我们有
在每次迭代中,得到最优$\lambda_2^\star$ , 根据问题(46)的等式约束,我们可以得到该次迭代中最优的$\lambda_1^\star$:
当在某次迭代中得到最优的解$\lambda_1^\star,\lambda_2^\star$ 后,根据公式(36)得到最优的$\mathrm w$ ,那么我们只需要更新$\omega_0$的值,从而可以确定分类超平面。我们更新$\omega_0$的宗旨就是使得$\lambda_1,\lambda_2$ 对应的KKT条件(42)满足。当$0<\lambda_i<C,i=1,2$ 时,此时 $\xi_i=0$,$(\omega_0+\mathrm w^{\mathrm T}\mathrm x_i)-1+\xi_i=0$。于是,我们有:
当$\lambdai=0, C, i=1,2$时,此时$\omega{0,1},\omega{0,2}$之间的值都满足KKT条件,为简便起见,我们取两者的中间值$\omega_0=\frac{\omega{0,1}+\omega_{0,2}}{2}$ 。

