0%

【图解例说机器学习】集成学习之AdaBoost算法

发表于 更新于
本文字数： 3.2k 阅读时长 ≈ 5 分钟

三个臭皮匠，顶个诸葛亮。

集成学习 (Ensemble learning) 通过构建并结合多个学习器来完成学习任务，即先产生一组个体学习器，再通过某种策略将它们结合起来完成学习任务。

个体学习器通常为一个现有的学习算法从训练数据产生，例如决策树，神经网络等。结合策略：在回归问题中，一般采用 (加权) 平均法，在分类问题中，一般采用 (加权) 投票法。当训练数据很多时，一种更为强大的结合策略为学习法，即通过另一个学习器来进行结合，典型代表为Stacking.

根据个体学习器的生成方式不同，目前的集成学习方法大致分为两大类：序列化方法和并行化方法。在序列化方法中，个体学习器之间存在强依赖关系，需要串行生成，其代表为Boosting；在并行化方法中，个体学习器间不存在强依赖关系，可同时生成，其代表为Bagging和随机森林 (Random Forest)。

本文主要介绍Boosting算法簇中最经典的代表AdaBoost。

AdaBoost

AdaBoost算法有多种推导方式，比较简单易懂的是基于加性模型，以指数函数为损失函数，优化方法为前向分步算法的推导。具体如下所示：

模型与损失函数

假设给定一个二分类的训练数据集$\mathcal D={(\mathrm x_i,y_i)\mid i=1,2,\cdots,N}$，总共有$K$个个体学习器$f_k(\mathrm x),k=1,2,\cdots,K$。此时，模型的表达式为：

这里我们采用指数损失函数：

我们的目标是优化参数$\alpha_k, f_k(\mathrm x)$使得损失函数最小，即

一般来说，优化问题(3)不易求解。我们可以采用前向分布算法逐一地学习个体学习器$f_k(\mathrm x)$, 具体操作如下：

在第$t$次迭代中，我们假设已经学习得到了$\alpha_k, f_k(\mathrm x),k=1,2,\cdots,t-1$, 根据公式(1)，我们有

根据公式(2)，此时的损失函数为：

注意：在公式(5)中，$w_{ti}$已经由前$t-1$次迭代得到。为此，为最小化当前的损失函数，我们可以对$\alpha_t$求导可得：

其中，我们有：

令公式(6)等于0，我们可得：

其中，分类误差率$e_t$可以表示为：

由公式(2)：

根据公式(5)中$w_{ti}$的定义可知

这里我们对$w_{t+1,i},i=1,2,\cdots,N$进行归一化，即：

由公式(9)可知，$w{ti}$可以看成是在$t$次迭代过程中，样例点$\mathrm x_i$的误差权重。$w{ti}$越大，说明越期望$\mathrm x_i$被正确分类，其被误分类的损失越大。

到目前为止，我们就完成了第$t$次迭代过程中需要更新的值：个体学习器$ft(x)$及其权重$\alpha_t$ ，以及下一次迭代时计算误差率(9)所需要的权重$\bar w{t+1,i}$。注意：这里的个体学习器$f_t(x)$可以是一些常见的算法，如决策树，神经网络等；另外，初始的权重值可以设置为$1/N$，即可把所有样例等同看待。

一个例子

如下表所示包含10个训练样例的训练集。假设个体分类器简单地设为$x<v$或者$x\ge v$，其阈值$v$使得该分类器在训练数据集上误分类率最低，这里我们可以采用穷举来得到。

$\mathrm x$ 0 1 2 3 4 5 6 7 8 9
$y$ 1 1 1 -1 -1 -1 1 1 1 -1

第$t=1$次迭代：

我们假设初始权值为

然后根据公式(9)和我们假定的分类器

通过穷举$v={-0.5,0.5,1.5,\cdots,9.5}$来找到最优的$v=2.5$使得误分类率(9)最小，即：

根据公式(8)和(15)，我们计算

至此，我们得到第$t=1$次的表达式：

(17)对应的分类函数为：

根据(18)，我们有

$\mathrm x$ 0 1 2 3 4 5 6 7 8 9
y 1 1 1 -1 -1 -1 1 1 1 -1
$\hat y$ 1 1 1 -1 -1 -1 $\color{red}-1$ $\color{red}-1$ $\color{red}-1$ -1

最后根据(12)来计算下次迭代所需要的权重：

第$t=2$次迭代：

然后根据公式(9)和我们假定的第二个分类器

通过穷举$v={-0.5,0.5,1.5,\cdots,9.5}$来找到最优的$v=8.5$使得误分类率(9)最小，即：

根据公式(8)和(21)，我们计算：

此时，我们得到第$t=2$次的表达式：

(23)对应的分类函数为：

根据(24)，我们有

$\mathrm x$ 0 1 2 3 4 5 6 7 8 9
y 1 1 1 -1 -1 -1 1 1 1 -1
$\hat y$ 1 1 1 $\color{red}1$ $\color{red}1$ $\color{red}1$ 1 1 1 -1

最后根据(12)来计算下次迭代所需要的权重：

第$t=3$次迭代：

然后根据公式(9)和我们假定的第三个分类器

通过穷举$v={-0.5,0.5,1.5,\cdots,9.5}$来找到最优的$v=5.5$使得误分类率(9)最小，即：

根据公式(8)和(27)，我们计算：

此时，我们得到第$t=3$次的表达式：

(29)对应的分类函数为：

根据(30)，我们有

$\mathrm x$ 0 1 2 3 4 5 6 7 8 9
y 1 1 1 -1 -1 -1 1 1 1 -1
$\hat y$ 1 1 1 -1 -1 -1 1 1 1 -1

最后根据(12)来计算下次迭代所需要的权重：

从上表可知，分类函数(30)已经能成功将这10个样例分类，实际上(31)已经不需要计算了。此时，最终的分类函数即为(30)。

具体算法实现

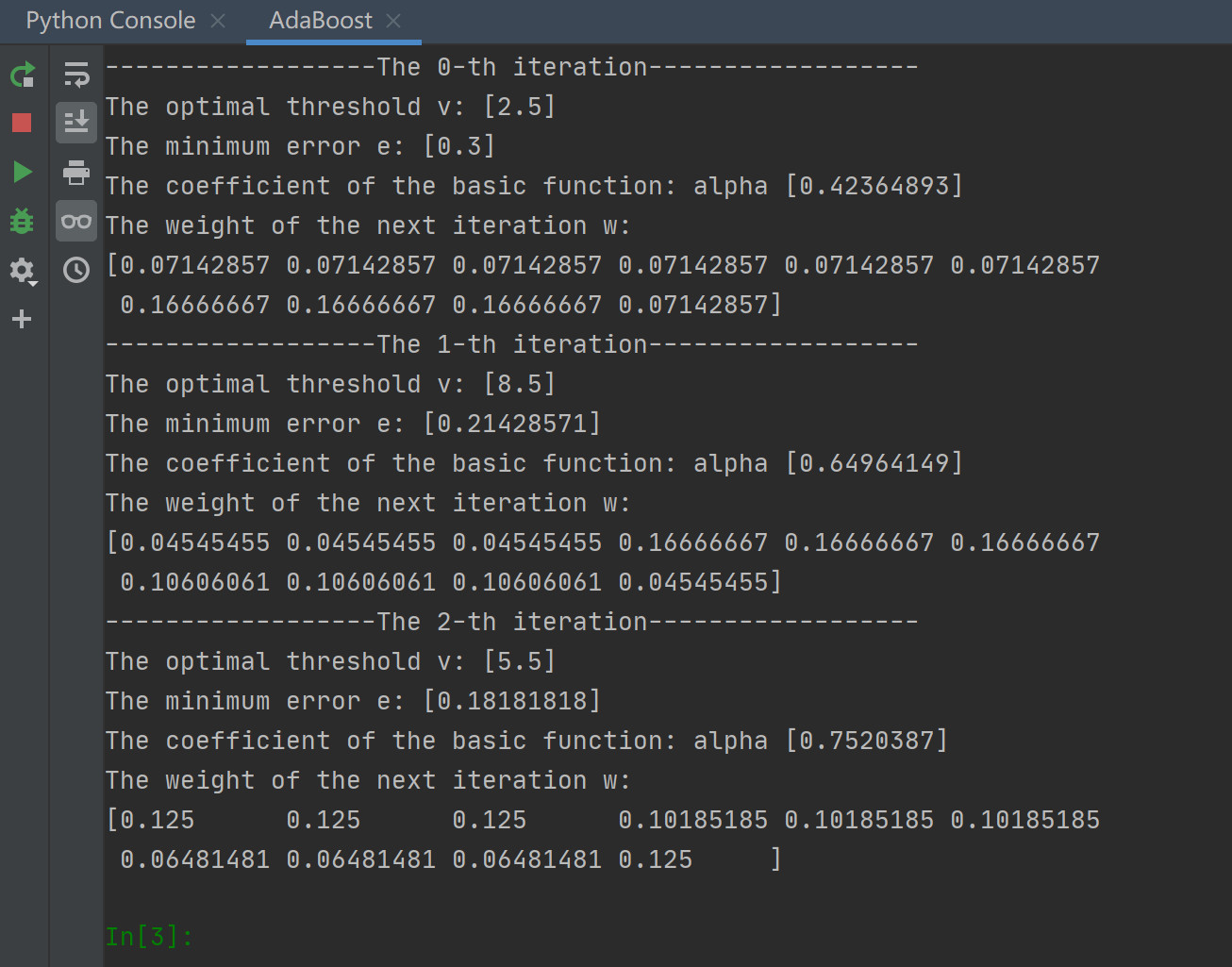
对于上面的例子，我们使用python进行了算法实践，其结果与上述过程相同，如图1：

图1

对应的Python源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
# -*- encoding: utf-8 -*-
"""
@File    : AdaBoost.py
@Time    : 2020/6/17 22:02
@Author  : tengweitw
@Email   : tengweitw@foxmail.com
"""

import numpy as np
import matplotlib.pyplot as plt

train_x = range(10)
train_y = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]

N = len(train_x)  # num of instances
K = 3  # num of basic classfier

w = np.zeros((K + 1, N))
alpha = np.zeros((K, 1))
v = np.zeros((K, 1))
f_t_x = np.zeros((K, 1))
# used for brute force
values = np.linspace(-0.5, 9.5, 11)


# exhaust search for the optimal threshold value
def Choose_values(values, w, train_x, train_y, N):
    error1 = []
    tmp1 = np.zeros((N, 1))
    tmp2 = np.zeros((N, 1))
    for v in values:
        tmp3 = 0
        for i in range(N):
            if (train_x[i] < v):
                tmp1[i] = 1
            else:
                tmp1[i] = -1
            if (tmp1[i] == train_y[i]):
                tmp2[i] = 0
            else:
                tmp2[i] = 1

            tmp3 = tmp3 + tmp2[i] * w[i]
        error1.append(tmp3)
    # Note that there are two cases: y=1,if x>v or y=-1, if x>v
    err_min1 = min(error1)
    err_min_index1 = error1.index(err_min1)

    error2 = []
    tmp1 = np.zeros((N, 1))
    tmp2 = np.zeros((N, 1))
    for v in values:
        tmp3 = 0
        for i in range(N):
            if (train_x[i] < v):
                tmp1[i] = -1
            else:
                tmp1[i] = 1
            if (tmp1[i] == train_y[i]):
                tmp2[i] = 0
            else:
                tmp2[i] = 1

            tmp3 = tmp3 + tmp2[i] * w[i]
        error2.append(tmp3)
    err_min2 = min(error2)
    err_min_index2 = error2.index(err_min2)

    if (err_min1 < err_min2):
        error = err_min1
        index = err_min_index1
        flag = 0  # case 0: y=1 if x<v
    else:
        error = err_min2
        index = err_min_index2
        flag = 1  # case 1: y=-1 if x<v

    return index, error, flag


for k in range(K):
    print('------------------The %d-th iteration------------------' % (k))
    if k == 0:
        for i in range(N):
            w[k][i] = 1.0 / N  # initialization: equal weigh

    v_index, err, flag = Choose_values(values, w[k], train_x, train_y, N)
    v[k] = values[v_index]
    alpha[k] = np.log((1 - err) / err) / 2.0
    print('The optimal threshold v:', v[k])
    print('The minimum error e:', err)
    print('The coefficient of the basic function: alpha', alpha[k])

    for i in range(N):
        if train_x[i] < v[k]:
            f_t_x = 1
        else:
            f_t_x = -1
        if flag == 1: # check case 0 or case 1
            f_t_x = -f_t_x
        w[k + 1][i] = w[k][i] * np.exp(-train_y[i] * alpha[k] * f_t_x)

    sum_tmp = sum(w[k + 1])
    for i in range(N):
        w[k + 1][i] = w[k + 1][i] / sum_tmp # regularization
    print('The weight of the next iteration w:')
    print(w[k + 1])
坚持原创技术分享，您的支持将鼓励我继续创作！