对于一个顶点数为N的有向网路图,我们可以通过前面所提到的单源最短路径算法执行N次来获得每一对顶点间的最短路径。这种方法的时间复杂度为$O(N^3)$。如果网络中有负权值的边,则需要使用前面提到的单源最短路径算法之Bellman—Floyd算法。总之,总可以通过单源最短路径来求得每对顶点间的最短路径。这里我就不再用程序实现上述方法。下面介绍Floyd解决这一问题的另一种算法,它形式简单,利于理解,而且时间复杂度同样为$O(N^3)$。
Floyd算法是根据给定有向网络的邻接矩阵$dist[n][n]$来求顶点$v_i$到顶点$v_j$的最短路径。这一算法的基本思想是:假设$v_i$和$v_j$之间存在一条路径,但这并不一定是最短路径,试着在$v_i$和$v_j$之间增加一个中间顶点$v_k$。 若增加$v_k$后的路径$(v_i, v_k, v_j)$ 比$(v_i, v_j)$短,则以新的路径代替原路径,并且修改$dist[i][j]$的值为新路径的权值;若增加$v_k$后的路径比$(v_i, v_j)$更长,则维持$dist[i][j]$不变。然后在修改后的$dist$矩阵中,另选一个顶点作为中间顶点,重复以上的操作,直到除$v_i$和$v_j$顶点的其余顶点都做过中间顶点为止。下面以具体实例来说明问题:
假设有向网路图如下所示:
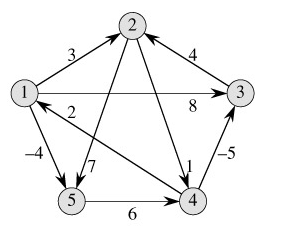
设原始的最短路径矩阵为$L^{(1)}$,经过一次循环后得到新的最短矩阵为$L^{(2)}$,依此类推,当得到$L^{(N-1)}$时,我们就得到了最短的路径矩阵。最短路径矩阵的变化情况如下:

具体程序实现如下:
1 |
|
结果显示如下:
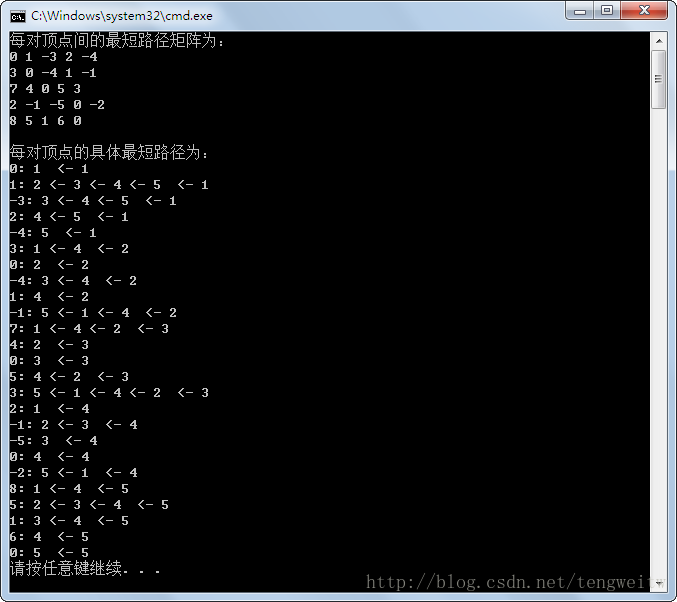
程序不但显示了两点之间的最短路径长度,而且显示了具体的路径。在程序中,我用了两种方法求最短路径矩阵,其中第二种方法更加简单的,因为我们要求的最短路径矩阵为$L^{(N-1)}$。比如说当$N=5$时,我们需要最终得到$L^{(4)}$,我们可以只求$L^{(1)}$、$L^{(2)}$、$L^{(4)}$,而不需要求得每一个$L$。

