感知机是二分类的线性分类模型,是神经网络和支持向量机的基础。
引例
一个常见的线性二分类问题如下:
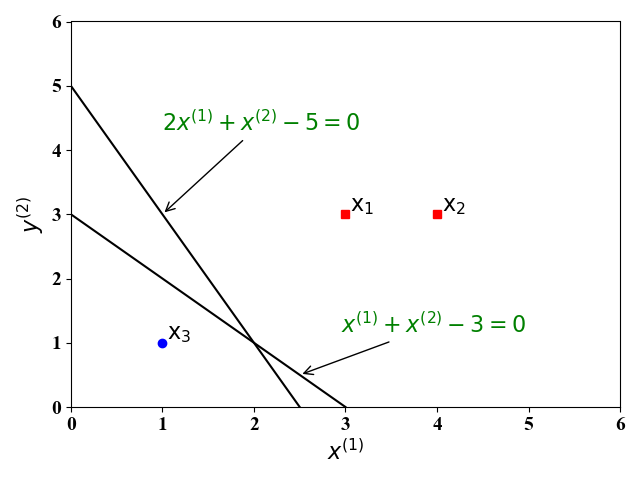
如图1,假设有一个线性可分的训练集,其中有三个样例 ($\mathrm x_1,\mathrm x_2, \mathrm x_3$),分别标记为正例(红色方块),反例(蓝色圆圈)。这里的 $x^{(1)},x^{(2)}$为训练样例的$2$个特征。我们的目的就是找到一个超平面 (在二维空间为一条直线) 能够将这三个样例分开。显然,这样的直线有无数条,比如图中的直线 $f(\mathrm x)=x^{(1)}+x^{(2)}-3=0, f(\mathrm x)=2x^{(1)}+x^{(2)}-5=0$ 就是其中的两条。我们发现$f(\mathrm x_1)>0,f(\mathrm x_2>0),f(\mathrm x_3)<0$,于是乎,我们可以用函数表达式$f(\mathrm x)$输出值的正负来判断新的样例$\mathrm x$属于哪一类。
定义
由上面的例子,我们可以得到下面关于感知机的数学表达式:
其中,$\mathbb I$是指示函数,定义为:
由公式(1),(2)可知,上面例子中,$f(\mathrm x_1)=f(\mathrm x_2=1>0),f(\mathrm x_3)=-1<0$。 注意:上述指示函数的取值为$-1,+1$是用来区分正例,反例。使用其它的值也是可以的。
误差函数
分类好坏的依据是能够将训练样例正确地分类,一个自然而然的误差函数就是分类错误数。但是,这样的误差函数不是连续的,不利于我们求解最优的。为此,我们考虑误分类点到分类超平面的距离,作为我们的误差函数。在中学时,我们学过一个点$x$到一条直线$ax+by+c=0$的距离可以为$\lvert ax+by+c\rvert/\sqrt{a^2+b^2}$。类似地,空间中一点$\mathrm x$ 到一个超平面$\omega_0+\mathrm w^{\mathrm T}\mathrm x=0$的距离为:
那么,对于误分类的样例$\mathrm x_i$,其预测的输出为$\hat y_i=f(\mathrm x_i)$。假定预测输出为负例,即$\hat y_i=-1$,由于被错误分类,其实际的输出为$y_i=+1$,其输入为$\omega_0+\mathrm w^{\mathrm T}\mathrm x_i>0$。为此,我们根据公式(3),可以计算当$\mathrm x_i$被误分类时,该点到分类超平面的距离为:
注意:公式(4)是公式(3)在误分类情况下的具体表达式。在误分类的情况下,输入$\omega0+\mathrm w^{\mathrm T}\mathrm x_i$ 与实际输出$y_i$ 异号。那么对于所有误分类的样例集合$\mathcal D{error}$,误差函数可以表示为:
一般来说,为了使用梯度下降求解最小化损失函数$E$方便,我们可以添加约束$\lvert\mathrm w\rvert=1$ 将公式(5)转化为:
然而,我们发现,约束$\lvert\mathrm w\rvert=1$ 对最终优化结果 (得到最优的分类超平面) 没有影响。以上面给的例子来说,比如对于一个给定的训练集$\mathrm x_1,\mathrm x_2,\mathrm x_3$,其最优的分类超平面为$f(\mathrm x)=x^{(1)}+x^{(2)}-3=0, \lvert\mathrm w\rvert=\sqrt{2}$ 。当添加约束$\lvert\mathrm w\rvert=1$ 后,此时可以求得最优的超平面一样,只是需要将参数归一化:$f(\mathrm x)/\sqrt{2}=x^{(1)}/\sqrt{2}+x^{(2)}/\sqrt{2}-3/\sqrt{2}=0, \lvert\mathrm w\rvert=\sqrt{2}$ 。为此,我们可以不用考虑约束$\lvert\mathrm w\rvert=1$。
梯度下降法求解问题
算法理论
为了找到最优的分类超平面$\hat y=f(\mathrm x)$, 我们需要最小化误差函数$E$来求得最佳的参数$\mathrm{\bar w}={\omega_0,\mathrm w}$。这里我们采用梯度下降法。分别求$E$关于$\omega_0,\omega_j$的偏导数:
由于偏导数只与被错误分类的样例有关,我们可以采用随机梯度下降法,即每次只用一个被错误分类的训练样例 (e.g., $\mathrm x_i$ ) 来更新参数:
公式(9)和(10)的直观解释:对于每一个被误分类的样例点,我们调整$\omega_0,\mathrm w$的值,使分类超平面朝着该误分类的样例点移动,从而减少该分类点到分界面的距离,即误差。
算法实现
我们还是以上面的例子来具体说明算法的具体步骤。这例子只考虑了2个特征$x^{(1)},x^{(2)}$,于是乎我们要求的分类超平面为一条直线$f(\mathrm x)=\omega_0+\omega_1x^{(1)}+\omega_2x^{(2)}$=0. 那么上述的随机梯度算法步骤如下:
初始化参数: $\omega_0^0=\omega_1^0=\omega_2^0=0,\eta^t=\eta=1$;
迭代过程:
根据当前得到的分类直线,从训练集中找到一个会被误分类(即$f(\mathrm x_i)y_i\le 0$)的样例;
比如,在第一次迭代时,$\mathcal x_1$被误分类。我们可以把样例$\mathrm x_1$代入公式(9)和(10)中,我们有:
此时得到的分类直线为$1+3x^{(1)}+3x^{(2)}=0$。
重复步骤2,直到训练集中找不到被误分类的训练样例。
最后得到该训练集的分类超平面为:
此时所求的表达式为:
注意:这里的分类超平面有很多,与初始化的值和在步骤2中选取被误分类样例的不同有关。例如,$-5+x^{(1)}+2x^{(2)}=0$也是一个分类超平面。
具体算法实现
这里我们以上面的例子以及iris数据集(sklearn库中自带)进行感知机二分类算法实现。
简单的例子
在上述的小例子中,输入为${\mathrm x_1=(3,3),\mathrm x_2=(3,4),\mathrm x_3=(1,1)}$ ,其类别为${y_1=+1,y_2=+1,y_3=-1}$。我们假定一个新的测试样例为$\mathrm x=(4,4)$,其实际类别为$y=+1$。采用上面提及的随机梯度算法,我们可以得到如图2的实验结果 (具体实现的python源代码见附录):
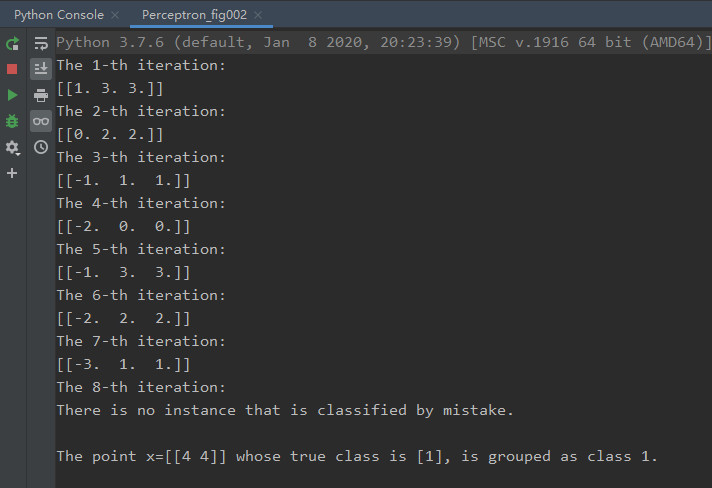
图2 Iris数据集
在iris数据集中,有150个训练样例,4个feature, 总共分3类。我们只考虑了前2个feature,这么做是为了在二维图3和图4中展示分类结果。并且将类别2和类别3划分为同一类别,这样我们考虑的是一个二分类问题。
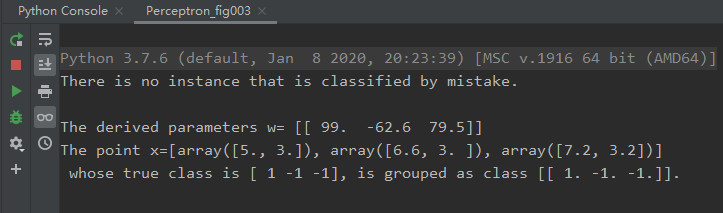 图3 图3 |
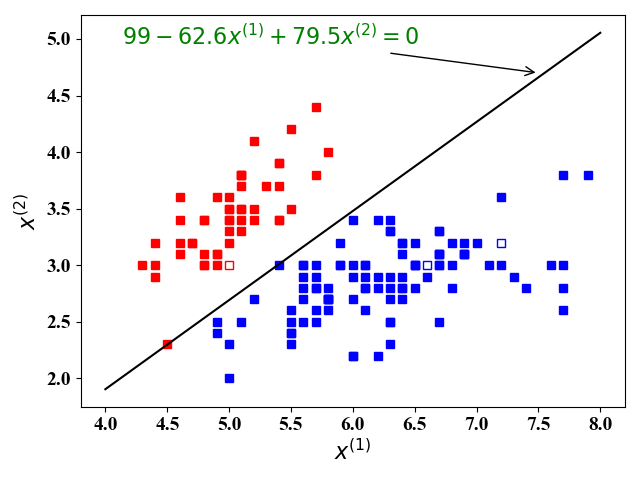 图4 图4 |
从图3和图4中可以看出,我们找到了一个分类直线$99-62.6x^{(1)}+79.5x^{(2)}=0$,可以正确对iris数据集正确分类。
附录
1 | # -*- coding: utf-8 -*- |
1 | # -*- coding: utf-8 -*- |
1 | # -*- coding: utf-8 -*- |

