在我们日常生活中,我们经常会遇到使用到预测的事例,而预测的值一般可以是连续的,或离散的。比如,在天气预报中,预测明天的最高温,最低温(连续),亦或是明天是否下雨(离散)。在机器学习中,预测连续性变量的模型称为回归(Regression)模型,比如标准的线性回归,多项式回归;预测离散型变量的模型称为分类(Classification)模型,比如这里要介绍的逻辑回归和以后要提到的支持向量机(SVM)等。
回归与分类的联系
根据上面的论述,回归与分类的区别在于预测的变量是否是连续的。具体来说,回归是求得一个函数$y=f(\mathrm x)$进行输入变量 $\mathrm x$ 到连续型输出变量 $y_r$ 的映射;分类是是求得一个函数$y=f(\mathrm x)$进行输入变量 $\mathrm x$ 到离散型输出变量 $y_c$ 的映射,可以将其看成是一个分段函数。
一个直觉的想法是,通过一个函数$y_c=g(y_r)$可以把回归模型转化为分类模型,即$y=g(f(x))$。逻辑回归正是用到了这一思想:逻辑回归是在回归模型的基础上,将回归模型的输出$y_r$映射成离散输出$y_c$,我想这也是为什么取名逻辑回归而不是逻辑分类吧。 需要注意,逻辑回归是用来解决分类问题的。
一个例子
如图1所示,假定我们有6个样本点,3个正例($y=1$)和3个反例($y=0$)。我们对其进行线性回归。当使用最简单的线性回归模型(即$\hat y=\omega_0+\omega_1x$)时,我们可以得到其最佳函数表达式为$\hat y=x$,如图中虚线所示。当我们使用复杂的回归模型时(比如考虑$x$的高阶项)时,此时我们可以得到一个十分接近$\hat y=\frac{1}{1+e^{-x}}$的函数表达式。显然,后者的效果更好,但是复杂度十分高。
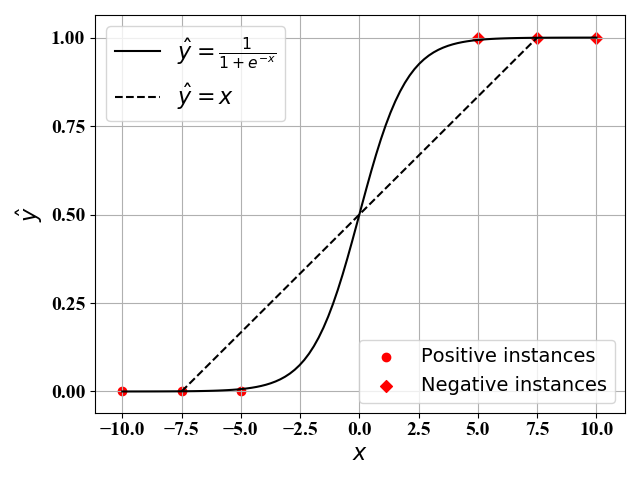
从分类问题的角度来看,我们并不关心每一个样例点的预测值,只是关心最终每个样例点属于哪一类。分类问题就是找到一个好的分段函数,使得输入$x$在不同区间的时候,输出$\hat y$分成不同类。比如图1中,当$x<0$时,判别为类别$0$;当$x>0$时,判别为类别$1$,于是我们有如下分段函数表达式:
分段函数(1)虽然形式简单,但是在$x=0$处不可导,不利于后面使用梯度下降法。为此,一般通过图1中的Sigmoid函数$\hat y=\frac{1}{1+e^{-x}}$来近似。
模型描述
在逻辑回归中,输入 $\mathrm x$ 与输出 $\hat y$ 的函数表达式为
其中,$\mathrm z=h(\mathrm x)=\omega_0+\mathrm{w^T}\phi(\mathrm x)$ 是线性回归的函数表达式,$g(\mathrm z)=[1+e^{-\mathrm z}]^{-1}$ 是Sigmoid函数。
注意:Sigmoid函数$g(\mathrm z)$的作用是将线性回归的输出$\mathrm z=h(\mathrm x)$映射到$0$到$1$的取值范围。
误差函数
损失函数有很多种选择:在线性回归中,我们一般采用的是最小均方误差,即$E=\sum_i{(\hat y_i-y_i)^2}$ 。然而在逻辑回归中,使用最小均方误差后,误差函数$E$对于变量$\mathrm w$不一定是凸函数,不利于求解。为此,有人提出了使用交叉熵作为误差函数:
问题求解
逻辑回归就是寻找一组参数 $\bar{\mathrm w}={\omega_0,\mathrm w}$ 使得误差函数值最小,即:
这是一个凸优化问题,和线性回归类似,我们可以考虑的方法有正规方程法和梯度下降法。但是由于该函数表达式比较复杂,正规方程法一般无法得到其解析解。为此,下面我们采用梯度下降法进行求解。
梯度下降法
梯度下降法的一般表达式如下:
对于每一个训练样例$\mathrm x_i$采用求导的链式法则,我们有:
将公式(1)和(2)带入可得
最终,逻辑回归问题的迭代表达式为
算法实现
我们这里使用iris数据集(sklearn库中自带),这里面有150个训练样例,4个feature, 总共分3类。我们只考虑了前2个feature,这么做是为了在二维图中展示分类结果。并且将类别2和类别3划分为同一类别,这样我们考虑的是一个二分类问题。
图2给出了使用梯度下降法时,误差的收敛情况。这里我们假设学习率 $\eta=1e^{-3}$,算法差不多需要迭代3000次左右收敛。
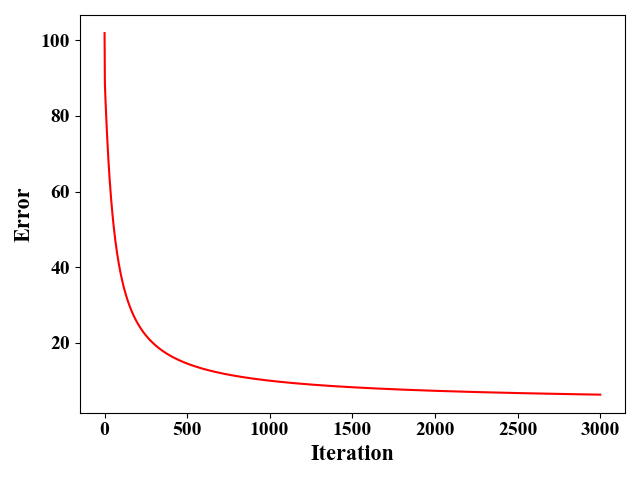
在这150个样例中,我们取出第25,75,125个样例作为测试样例(其label分别为0,1,1),其他147个作为训练样例。下图为测试结果:
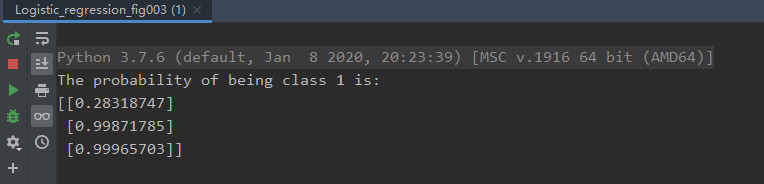
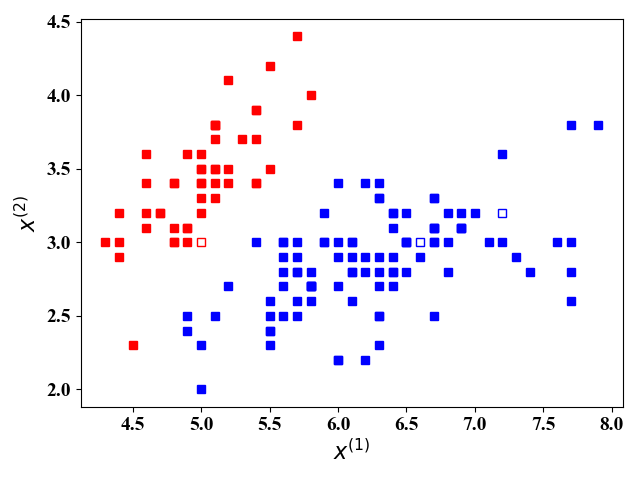
图4给出了这3三个测试样例的预测结果,其输出$\hat y$就是这3个测试样例属于类别 $1$ 的概率。当$\hat y>0.5$时,判别为$1$,否则判别为$0$。图5更加直观地显示了图4的判别结果。其中,空心方块即为我们要预测的点,颜色代表所处类别,红色为类别$0$,蓝色为类别$1$,可见,我们对于这个三个点的预测正确。
附录:
这里我们给出图1-图4的Python源代码
1 | # -*- coding: utf-8 -*- |
1 | # -*- coding: utf-8 -*- |

